
What does this AI generated picture of a donkey in space have to do with uncertainty? Read on to find out!
Welcome to the second installment of “Decisions in board games”, a three-part series on engaging players through meaningful decisions in competitive multiplayer board games. Previously we discussed why decisions are important and why you should have them in your game. If you haven’t checked that out yet, I recommend reading it first. In this post we will dive deeper into what really makes decisions “meaningful”. The third and final post will share a number of examples from Legends of the Arena and how we applied board game decision theory to create a more engaging experience for players.
Uncertainty about gameplay consequences is necessary to make decisions in board games meaningful. Players manage uncertainty via valuation and reading. Understanding and designing for these techniques is crucial when manifesting interesting gameplay consequences in your game. Each of these concepts probably deserves a post of its own, but I will attempt to summarize them in brief here and offer references for those who wish to read more.
Uncertainty
A game element is considered to be uncertain if it is not known to at least one player. This could be an outcome like the roll of the dice or the contents of another player’s hand. Competitive players often strive to divine their opponents' hidden information while veiling their own actions in a layer of uncertainty.
Greg Costikyan’s Uncertainty in Games is the best resource for delving further into this topic. For a lighter treatment this article summarizes Greg’s classification. For multiplayer board games without dexterity or other physical skill elements we can focus on just a few:
- Randomness: Have random elements like a deck or dice (e.g. poker)
- Analytic complexity: Overload the players with so many possibilities and possible futures that they can’t compute what is going on (e.g. chess)
- Player unpredictability: Use the other players to introduce uncertainty (e.g. simultaneous decisions, auctions).
Now that we have a working model of uncertainty, let’s look into how players seek to unwind that uncertainty for their own benefit.
Valuation
Valuation is figuring out which option is best based on the expected value. The best option could be the number of victory points you’ll receive or the amount of damage you’ll deal. This doesn’t have to be a certain thing; if one option gives you an 80% chance of scoring 1 point and the other option gives you a 20% chance of scoring 2 points the choice is quite clear (in most situations). If you are interested in more detail, R. Eric Reuss (designer of Spirit Island) has a good primer on valuation in board games.
Valuation can quickly become impractical - if it takes many turns and intermediate uncertain elements to reach a payoff players may not be able to perfectly compute the valuation (see analytic complexity above). However, players will still attempt to compute expectations, and the players that are better at doing so will have an advantage over other players. The players that perform valuation exercises with more skill than others are able to reduce uncertainty for themselves so they can make better decisions.
Valuation is a double-edged sword for designers. Generally players really like doing valuation exercises. Those exercises make players feel smart and give them the impression that they are making informed decisions. When encountering a new game, players will often feel the rush of discovery as they work through the valuation exercises for the first time. Novelty is a huge part of games - after all, many games only get a few plays before they are permanently relegated to the shelf.
The negative side of valuation is that games which heavily rely on players computing expectations become more inaccessible with repeated plays, and, in some cases, break entirely. Playing chess at a high level requires years of intense study to memorize all of the valuations that players have previously computed and written down. A new player doesn’t stand a chance against a veteran.
Reading
If valuation is how players address analytic complexity, then reading is how they handle player unpredictability. Reading is understanding the mind of the opponent; understanding their biases and strategy. David Sirlin (designer of Yomi) writes about reading in his article on solvability (note that some of his terminology differs from what you will see here).

The thought process behind reading the opponent is comically demonstrated in The Princess Bride when Vizzini monologues at length about which chalice is poisoned.
Virtually all games played at a high level exhibit some form of reading. Once all players have mastered the basics of valuation, they cannot rely on merely playing more efficiently than their opponents in order to win. Many games have some sort of rock-paper-scissors at their core (e.g. turtle/rush/boom in a real-time strategy game). If you can figure out which option your opponent has chosen then victory is much more probable.
Designing donkeyspace
Now, let’s talk about how a designer can influence reading and valuation to ensure that their game has meaningful decisions. In cooperative or solo games, analytic complexity on its own is often enough to create meaningful decisions. However, as we’ve discussed, in multiplayer competitive games analytic complexity can devolve into a simple test of memorization or ability to compute ahead a few turns. What can a designer do to make sure decisions are still meaningful? First, we need to introduce another term, donkeyspace.
What is donkeyspace?
Frank Lantz coined the term donkeyspace:
Imagine all the possible strategies you could be up against plotted in a multidimensional space, over here is the “perfect” strategy, unexploitable, there’s nothing you can do against it but play it yourself. But all around it are the vast, diverse spectrum of sub-optimal strategies that people actually use. This is Donkeyspace, and your goal is to place your opponent as accurately as possible at a point in this space, and then maneuver yourself to the point that takes maximal advantage of him.
From the designer’s perspective, donkeyspace is the universe of sub-optimal strategies in your game. If your game has any degree of analytical complexity, it probably has lots of sub-optimal strategies. The perfect strategy is likely not known and may never be discovered (at least not in a reasonable timeframe). When players are aware that they are in donkeyspace, they are competitively outguessing each others' strategies. There is uncertainty, and, more importantly, there is meaningful choice.
Decisions that require players to read their opponents are made in donkeyspace. To get to that point, the “decision space” must contain at least two options that cannot be practically eliminated through valuation. Decisions in donkeyspace are inherently meaningful because there is no way to calculate a simple answer.
So - we want meaningful decisions in our game, and putting our players in donkeyspace is one way to make sure their decisions are meaningful. How do we go about encouraging donkeyspace?
Decide when your game should send players into donkeyspace
In most games, donkeyspace is only possible for a portion of the game. That isn’t a bad thing; working through donkeyspace can be exhausting. Many fun parts of games don’t involve intense mental concentration.
For most games, you should strive for the end to be in donkeyspace. Once a player is mathematically eliminated from a game, the game tends to lose interest for that player. By definition, there is no point in reading the opponent if all outcomes are the same. However, the designer must decide how far donkeyspace extends towards the start of the game (and whether it comes and goes throughout).
In the early game, players like exploring different options and building up their position, so it isn’t strictly necessary to have meaningful decisions. In fact, there is some risk to making early decisions too meaningful. Consider the case of early picks in a deckbuilding game. If those picks lock the player into a certain strategy the rest of their decisions are less meaningful since they are simply executing the pre-determined strategy. In the worst case donkeyspace ends completely after strategies are chosen - the rest of the game is “on rails”. To combat this, include off-ramps to change strategies or otherwise react to what opponents are doing.
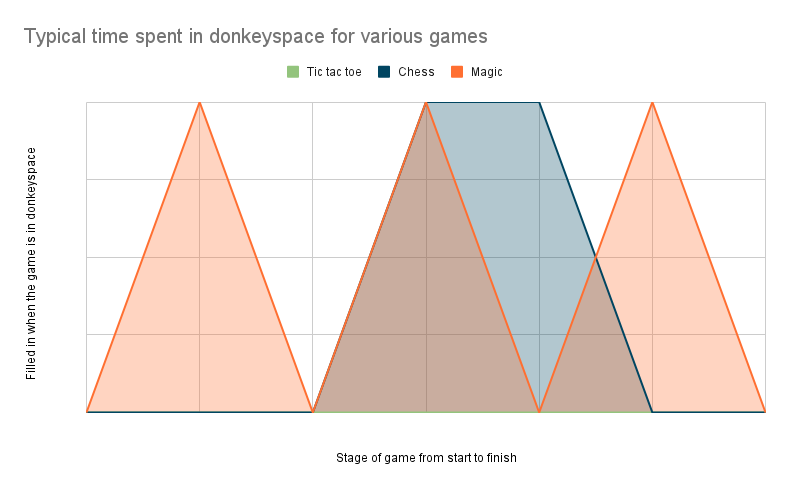
This graph is a representative image to show how donkeyspace appears in different games. Tic-tac-toe is fully solved so donkeyspace is never present. Chess is solved during the opening and endgame, but it is often in donkeyspace in the midgame. Magic: The Gathering oscillates in and out of donkeyspace; there are sequences of straightforward play punctuated by exciting moments in which players must choose a particular line from multiple viable options.
Output randomness
Valuation addresses analytic complexity and reading addresses player unpredictability. But what of randomness, the third source of uncertainty in typical board games? Players don’t have a general tool to address randomness, so designers can fall back on randomness to keep decisions meaningful when they otherwise would not be.
In particular, output randomness is a useful tool because it gives the opportunity for players to have different mental models of how to hedge bets (and different models of each others' strategies). This is in contrast to input randomness which is usually managed by valuation - for example, in a dice game where the player is tasked with selecting a number of dice to use from a pool of dice they rolled. Output randomness is not guaranteed to put players into donkeyspace, but it is effective when the stakes are high enough and both players have a number of ways to hedge their bets.
As long as the ultimate outcome of the game is uncertain, there is the opportunity for meaningful decisions. Here’s a classic Magic: The Gathering topdeck from 2006 in which the game was in the balance until the last possible moment. The game was decided by chance, but the players made decisions which were justified by the uncertainty of that last card.
Randomize setup
One case in which input randomness does encourage donkeyspace is randomized setups. Randomized setups add meaningful decisions, particularly near the start of your game, because players cannot memorize optimal opening strategies. Games with shuffled decks have this property by default, but other games can achieve a random setup as well (e.g. draw tiles from a bag) . Random setups still allow players to perform valuation exercises and provide a rush of novelty, but they don’t reward straight memorization. Due to the extreme analytic complexity of working out the end of the game from a given random setup, it is safe to say that random setups typically push players into donkeyspace. Chess960 is a great example of how radically a game can be transformed with just a randomized setup
Simultaneous play
When players make decisions at the same time, they are almost always thrust into donkeyspace. In contrast to standard, serialized play (where one player makes a choice and then the next player makes a choice) both players must consider the full range of possible outcomes. Unless the valuation of these options is extremely straightforward, players will virtually always be forced to consider the mind of their opponent.
We’ll discuss more on simultaneous play in a future post. This is an area we explored heavily in Legends of the Arena, but I find simultaneous play to be unfortunately underused in board game design.
Give players asymmetric information
Serialized play can prevent donkeyspace if a player’s entire intentions are revealed when they make a choice. If there is no remaining doubt about what that player is doing, their opponent simply performs a valuation exercise to determine the most efficient way to counter. As a designer, you can avoid this by letting players keep some important information in reserve (e.g. a hand of cards). As long as a player’s visible plays could correspond to multiple strategies, there is still the possibility for uncertainty, leading to donkeyspace.
Combined with output randomness
Output randomness, discussed above, is one method to bring some of the effects of simultaneous play into a serialized game. If the outcome becomes known to both players at the same time, but their decisions are locked in ahead of time, there is some room for donkeyspace to develop. This has a multiplicative effect when combined with asymmetric information - the less players can compute the valuation behind their opponents' moves, the more they are forced to consider their opponents' strategies and biases directly.
Consider a simple game in the style of Magic: The Gathering in which players have health totals (first to run out loses) and can be dealt damage by creatures. Each player takes turns attacking the other player with creatures that each deal some fixed amount of damage. Players can block incoming creatures with their own creatures, in which case the creatures damage each other. The weaker creature is destroyed and the stronger creature is unscathed.
Clearly this game has no donkeyspace. Both players can compute exactly what will happen given a sequence of attacks.
But what happens when we add asymmetric information? Perhaps players have hidden hands of cards that they can play. If the attacker has a card which rewards them for each creature that was destroyed this turn, they might make an attack with a weak creature, knowing that the defender can block and destroy their creature. The defender must decide whether to take damage from this weak creature, or block it and risk unlocking a powerful effect. Maybe this is just a bluff and the weak attack is a bid to sneak in some damage!
| Attacker gets rewarded for destroyed creatures | Attacker is bluffing | |
|---|---|---|
| Defender blocks | Wrong move for the defender? Attacker gains a powerful effect - but at least the attacker has used up their effect and lost a creature | Right move for the defender; defender takes no damage and destroyed the incoming creature |
| Defender does not block | Right move for the defender? Attacker doesn’t get a powerful effect - but they still dealt damage and they have the effect and creature for future turns | Wrong move for the defender; defender takes some damage |
Mentally, both the attacker and defender must approximate the valuation of each of these possible outcomes. However, the rewards are extremely difficult to quantify because they are based on the estimated future value of keeping the powerful effect in hand and the creature on the board. Even if the defender is pretty sure that the attacker should only make this attack if they have an effect in hand to take advantage of the destruction of the creature, the defender may assess that the attacker would bluff based on the attacker’s personal style. But maybe the attacker has cultivated that impression purely to trick the defender! So the attacker and defender find themselves in donkeyspace.
Let’s add output randomness as well. In this version, creatures deal damage based on dice rolls, with strong creatures rolling more dice. Now there is an additional possibility - the attacker might be hoping to roll well and win the combat outright! This makes it even harder for the defender to understand exactly what their opponent is planning, because calling the attacker’s bluff is no guarantee of success.
Hidden victory conditions
Hidden victory conditions are a great way to use a little bit of asymmetric information to create donkeyspace throughout the course of a game. Consider Lords of Waterdeep, in which each player is assigned a Lord that grants them bonuses for completing certain types of quests. Because victory conditions have such an outsized impact on the overall course of the game, they aren’t easily ignored or discounted. When choosing whether to take a location that is useful or block an opponent from a location they desperately need, you must consider how much that location is worth to the opponent – but without knowledge of their hidden victory condition your valuation is at best approximate and can be exploited by a cunning foe.
Conclusion
We began by introducing uncertainty and showed how players use reading and valuation to manage that uncertainty. Then we introduced donkeyspace as a term for the space of suboptimal strategies in a game. Donkeyspace thrives when there is uncertainty and collapses when the best move is easily calcualted. When both players are aware that they are in donkeyspace, they must read each other to gain an advantage. In this state, players are making meaningful decisions. Finally, we discussed a few options for how to push players into donkeyspace in your game. In the next article we will discuss specific examples of how we explicitly designed meaningful decisions into Legends of the Arena. Until then, please comment below if you know of any other techniques for encouraging donkeyspace or games that do this particularly well!